Pan ddaw iantenâu, y cwestiwn y mae pobl yn poeni fwyaf amdano yw "Sut mae ymbelydredd yn cael ei gyflawni mewn gwirionedd?" Sut mae'r maes electromagnetig a gynhyrchir gan y ffynhonnell signal yn lledaenu trwy'r llinell drosglwyddo a thu mewn i'r antena, ac yn olaf yn "gwahanu" oddi wrth yr antena i ffurfio ton gofod rhydd.
1. Ymbelydredd gwifren sengl
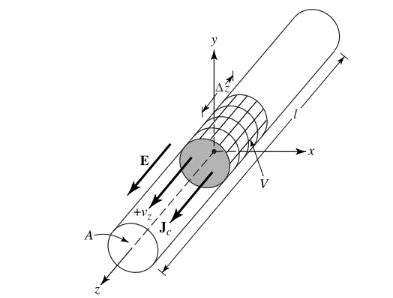
Gadewch inni dybio bod y dwysedd gwefr, a fynegir fel qv (Coulomb/m3), wedi'i ddosbarthu'n unffurf mewn gwifren gylchol gydag arwynebedd trawsdoriadol o a a chyfaint o V, fel y dangosir yn Ffigur 1.
Ffigur 1
Mae cyfanswm y gwefr Q yn y gyfaint V yn symud i gyfeiriad z ar gyflymder unffurf Vz (m/s). Gellir profi mai'r dwysedd cerrynt Jz ar drawstoriad y wifren yw:
Jz = qv vz (1)
Os yw'r wifren wedi'i gwneud o ddargludydd delfrydol, y dwysedd cerrynt Js ar wyneb y wifren yw:
Js = qs vz (2)
Lle mae qs yn cynrychioli dwysedd gwefr yr wyneb. Os yw'r wifren yn denau iawn (yn ddelfrydol, mae'r radiws yn 0), gellir mynegi'r cerrynt yn y wifren fel:
Iz = ql vz (3)
Lle mae ql (coulomb/metr) yn cynrychioli'r gwefr fesul uned o hyd.
Rydym yn ymwneud yn bennaf â gwifrau tenau, ac mae'r casgliadau'n berthnasol i'r tri achos uchod. Os yw'r cerrynt yn amrywio yn ôl amser, mae deilliad fformiwla (3) mewn perthynas ag amser fel a ganlyn:
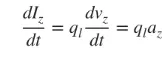
(4)
az yw cyflymiad y gwefr. Os yw hyd y wifren yn l, gellir ysgrifennu (4) fel a ganlyn:
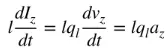
(5)
Hafaliad (5) yw'r berthynas sylfaenol rhwng cerrynt a gwefr, a hefyd y berthynas sylfaenol rhwng ymbelydredd electromagnetig. Yn syml, i gynhyrchu ymbelydredd, rhaid bod cerrynt neu gyflymiad (neu arafiad) gwefr sy'n amrywio yn ôl amser. Fel arfer, rydym yn sôn am gerrynt mewn cymwysiadau harmonig amser, a cheir y gair gwefr amlaf mewn cymwysiadau dros dro. Er mwyn cynhyrchu cyflymiad (neu arafiad) gwefr, rhaid plygu, plygu a bod yn anghyson. Pan fydd y gwefr yn osgiliadu mewn symudiad harmonig amser, bydd hefyd yn cynhyrchu cyflymiad (neu arafiad) gwefr cyfnodol neu gerrynt sy'n amrywio yn ôl amser. Felly:
1) Os nad yw'r gwefr yn symud, ni fydd cerrynt nac ymbelydredd.
2) Os yw'r gwefr yn symud ar gyflymder cyson:
a. Os yw'r wifren yn syth ac yn anfeidraidd o hyd, nid oes ymbelydredd.
b. Os yw'r wifren wedi'i phlygu, wedi'i phlygu, neu'n anghyson, fel y dangosir yn Ffigur 2, mae yna ymbelydredd.
3) Os bydd y gwefr yn osgiliadu dros amser, bydd y gwefr yn pelydru hyd yn oed os yw'r wifren yn syth.
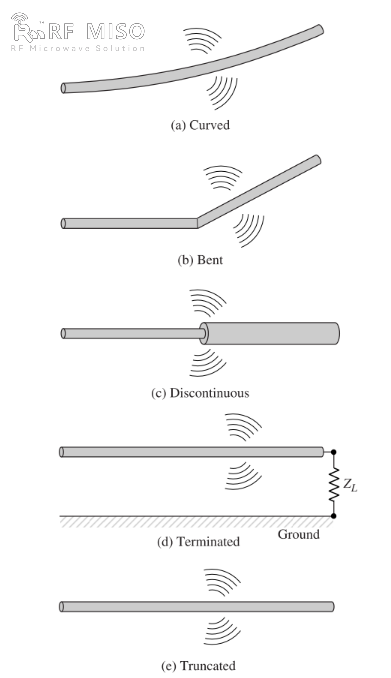
Ffigur 2
Gellir cael dealltwriaeth ansoddol o'r mecanwaith ymbelydredd drwy edrych ar ffynhonnell byrlymus sydd wedi'i chysylltu â gwifren agored y gellir ei seilio drwy lwyth yn ei phen agored, fel y dangosir yn Ffigur 2(d). Pan gaiff y wifren ei hegnio i ddechrau, mae'r gwefrau (electronau rhydd) yn y wifren yn cael eu rhoi ar waith gan y llinellau maes trydan a gynhyrchir gan y ffynhonnell. Wrth i'r gwefrau gael eu cyflymu ar ben ffynhonnell y wifren a'u harafu (cyflymiad negyddol o'i gymharu â'r symudiad gwreiddiol) pan gânt eu hadlewyrchu yn ei phen, cynhyrchir maes ymbelydredd ar ei bennau ac ar hyd gweddill y wifren. Cyflawnir cyflymiad y gwefrau gan ffynhonnell rym allanol sy'n rhoi'r gwefrau ar waith ac yn cynhyrchu'r maes ymbelydredd cysylltiedig. Cyflawnir arafiad y gwefrau ar bennau'r wifren gan rymoedd mewnol sy'n gysylltiedig â'r maes ysgogedig, a achosir gan groniad gwefrau crynodedig ar bennau'r wifren. Mae'r grymoedd mewnol yn ennill egni o groniad gwefr wrth i'w chyflymder ostwng i sero ar bennau'r wifren. Felly, cyflymiad y gwefrau oherwydd cyffroi'r maes trydanol ac arafiad y gwefrau oherwydd anghysondeb neu gromlin llyfn impedans y wifren yw'r mecanweithiau ar gyfer cynhyrchu ymbelydredd electromagnetig. Er bod dwysedd cerrynt (Jc) a dwysedd gwefr (qv) yn dermau ffynhonnell yn hafaliadau Maxwell, ystyrir bod gwefr yn faint mwy sylfaenol, yn enwedig ar gyfer meysydd dros dro. Er bod yr esboniad hwn o ymbelydredd yn cael ei ddefnyddio'n bennaf ar gyfer cyflyrau dros dro, gellir ei ddefnyddio hefyd i esbonio ymbelydredd cyflwr cyson.
Argymhellwch sawl un rhagorolcynhyrchion antenawedi'i gynhyrchu ganRFMISO:
2. Ymbelydredd dwy wifren
Cysylltwch ffynhonnell foltedd â llinell drosglwyddo dau ddargludydd sydd wedi'i chysylltu ag antena, fel y dangosir yn Ffigur 3(a). Mae rhoi foltedd ar y llinell ddwy wifren yn cynhyrchu maes trydan rhwng y dargludyddion. Mae'r llinellau maes trydan yn gweithredu ar yr electronau rhydd (sy'n hawdd eu gwahanu oddi wrth atomau) sydd wedi'u cysylltu â phob dargludydd ac yn eu gorfodi i symud. Mae symudiad gwefrau yn cynhyrchu cerrynt, sydd yn ei dro yn cynhyrchu maes magnetig.
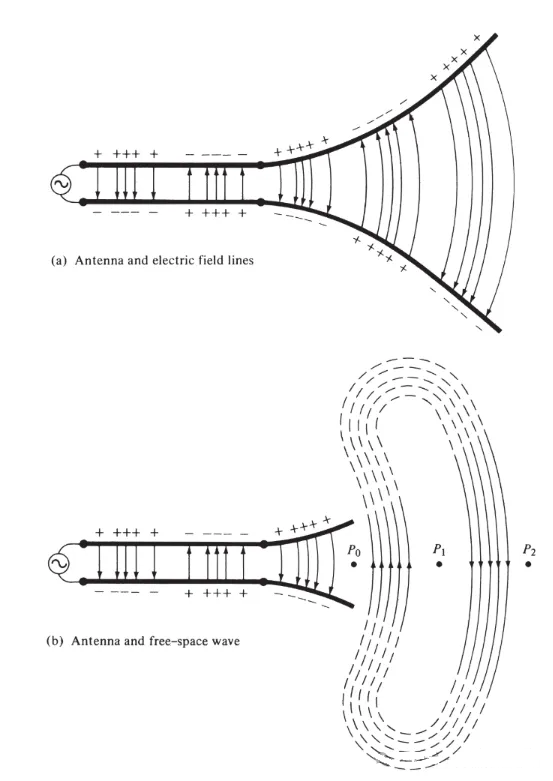
Ffigur 3
Rydym wedi derbyn bod llinellau maes trydanol yn dechrau gyda gwefrau positif ac yn gorffen gyda gwefrau negatif. Wrth gwrs, gallant hefyd ddechrau gyda gwefrau positif a gorffen ar anfeidredd; neu ddechrau ar anfeidredd a gorffen gyda gwefrau negatif; neu ffurfio dolenni caeedig nad ydynt yn dechrau nac yn gorffen gydag unrhyw wefrau. Mae llinellau maes magnetig bob amser yn ffurfio dolenni caeedig o amgylch dargludyddion sy'n cario cerrynt oherwydd nad oes unrhyw wefrau magnetig mewn ffiseg. Mewn rhai fformwlâu mathemategol, cyflwynir gwefrau magnetig cyfatebol a cheryntau magnetig i ddangos y ddeuoldeb rhwng atebion sy'n cynnwys pŵer a ffynonellau magnetig.
Mae'r llinellau maes trydan a dynnwyd rhwng dau ddargludydd yn helpu i ddangos dosbarthiad y gwefr. Os ydym yn tybio bod y ffynhonnell foltedd yn sinwsoidaidd, rydym yn disgwyl i'r maes trydan rhwng y dargludyddion hefyd fod yn sinwsoidaidd gyda chyfnod sy'n hafal i gyfnod y ffynhonnell. Cynrychiolir maint cymharol cryfder y maes trydan gan ddwysedd y llinellau maes trydan, ac mae'r saethau'n nodi'r cyfeiriad cymharol (positif neu negatif). Mae cynhyrchu meysydd trydan a magnetig sy'n amrywio yn ôl amser rhwng y dargludyddion yn ffurfio ton electromagnetig sy'n lledaenu ar hyd y llinell drosglwyddo, fel y dangosir yn Ffigur 3(a). Mae'r don electromagnetig yn mynd i mewn i'r antena gyda'r gwefr a'r cerrynt cyfatebol. Os ydym yn tynnu rhan o strwythur yr antena, fel y dangosir yn Ffigur 3(b), gellir ffurfio ton gofod rhydd trwy "gysylltu" pennau agored y llinellau maes trydan (a ddangosir gan y llinellau dotiog). Mae'r don gofod rhydd hefyd yn gyfnodol, ond mae'r pwynt cyfnod cyson P0 yn symud allan ar gyflymder golau ac yn teithio pellter o λ/2 (i P1) mewn hanner cyfnod o amser. Ger yr antena, mae'r pwynt cyfnod cyson P0 yn symud yn gyflymach na chyflymder golau ac yn agosáu at gyflymder golau mewn pwyntiau ymhell o'r antena. Mae Ffigur 4 yn dangos dosbarthiad maes trydan gofod rhydd yr antena λ∕2 ar t = 0, t/8, t/4, a 3T/8.
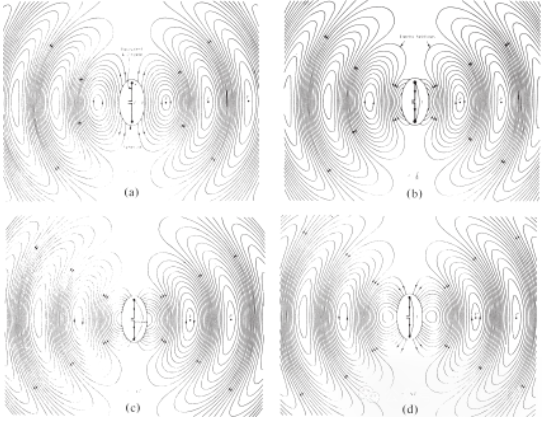
Ffigur 4 Dosbarthiad maes trydan gofod rhydd yr antena λ∕2 ar t = 0, t/8, t/4 a 3T/8
Nid yw'n hysbys sut mae'r tonnau tywysedig yn cael eu gwahanu oddi wrth yr antena ac yn y pen draw yn cael eu ffurfio i ledaenu mewn gofod rhydd. Gallwn gymharu tonnau tywysedig a thonnau gofod rhydd â thonnau dŵr, a all gael eu hachosi gan garreg a ollyngir mewn corff dŵr tawel neu mewn ffyrdd eraill. Unwaith y bydd yr aflonyddwch yn y dŵr yn dechrau, cynhyrchir tonnau dŵr ac maent yn dechrau lledaenu allan. Hyd yn oed os bydd yr aflonyddwch yn dod i ben, nid yw'r tonnau'n dod i ben ond yn parhau i ledaenu ymlaen. Os yw'r aflonyddwch yn parhau, cynhyrchir tonnau newydd yn gyson, ac mae lledaeniad y tonnau hyn yn llusgo ar ôl y tonnau eraill.
Mae'r un peth yn wir am donnau electromagnetig a gynhyrchir gan aflonyddwch trydanol. Os yw'r aflonyddwch trydanol cychwynnol o'r ffynhonnell yn fyr ei hyd, mae'r tonnau electromagnetig a gynhyrchir yn lluosogi y tu mewn i'r llinell drosglwyddo, yna'n mynd i mewn i'r antena, ac yn olaf yn pelydru fel tonnau gofod rhydd, er nad yw'r cyffroi yn bresennol mwyach (yn union fel y tonnau dŵr a'r aflonyddwch a greon nhw). Os yw'r aflonyddwch trydanol yn barhaus, mae'r tonnau electromagnetig yn bodoli'n barhaus ac yn dilyn yn agos ar eu hôl yn ystod y lluosogi, fel y dangosir yn yr antena biconig a ddangosir yn Ffigur 5. Pan fydd tonnau electromagnetig y tu mewn i linellau trosglwyddo ac antenâu, mae eu bodolaeth yn gysylltiedig â bodolaeth gwefr drydanol y tu mewn i'r dargludydd. Fodd bynnag, pan fydd y tonnau'n cael eu pelydru, maent yn ffurfio dolen gaeedig ac nid oes gwefr i gynnal eu bodolaeth. Mae hyn yn ein harwain i'r casgliad bod:
Mae cyffroi'r maes yn gofyn am gyflymiad ac arafiad y gwefr, ond nid yw cynnal y maes yn gofyn am gyflymiad ac arafiad y gwefr.
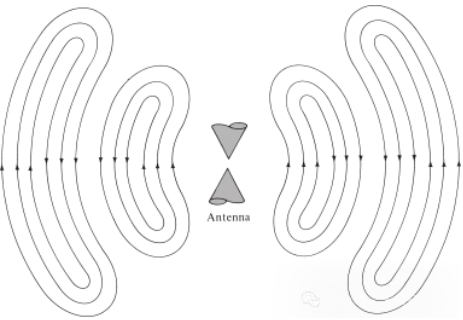
Ffigur 5
3. Ymbelydredd Dipol
Rydym yn ceisio egluro'r mecanwaith y mae'r llinellau maes trydan yn torri i ffwrdd o'r antena ac yn ffurfio tonnau gofod rhydd, a chymryd yr antena deupol fel enghraifft. Er ei fod yn esboniad symlach, mae hefyd yn galluogi pobl i weld yn reddfol gynhyrchu tonnau gofod rhydd. Mae Ffigur 6(a) yn dangos y llinellau maes trydan a gynhyrchir rhwng dwy fraich y deupol pan fydd y llinellau maes trydan yn symud allan λ∕4 yn chwarter cyntaf y cylch. Ar gyfer yr enghraifft hon, gadewch inni dybio bod nifer y llinellau maes trydan a ffurfiwyd yn 3. Yn chwarter nesaf y cylch, mae'r tair llinell maes trydan wreiddiol yn symud λ∕4 arall (cyfanswm o λ∕2 o'r man cychwyn), ac mae dwysedd y gwefr ar y dargludydd yn dechrau lleihau. Gellir ystyried ei fod wedi'i ffurfio trwy gyflwyno gwefrau cyferbyniol, sy'n canslo'r gwefrau ar y dargludydd ar ddiwedd hanner cyntaf y cylch. Mae'r llinellau maes trydan a gynhyrchir gan y gwefrau cyferbyniol yn 3 ac yn symud pellter o λ∕4, a gynrychiolir gan y llinellau dotiog yn Ffigur 6(b).
Y canlyniad terfynol yw bod tair llinell maes trydan tuag i lawr yn y pellter λ∕4 cyntaf a'r un nifer o linellau maes trydan tuag i fyny yn yr ail bellter λ∕4. Gan nad oes gwefr net ar yr antena, rhaid gorfodi'r llinellau maes trydan i wahanu oddi wrth y dargludydd a chyfuno gyda'i gilydd i ffurfio dolen gaeedig. Dangosir hyn yn Ffigur 6(c). Yn yr ail hanner, dilynir yr un broses ffisegol, ond nodwch fod y cyfeiriad yn groes. Ar ôl hynny, ailadroddir y broses ac mae'n parhau am gyfnod amhenodol, gan ffurfio dosbarthiad maes trydan tebyg i Ffigur 4.
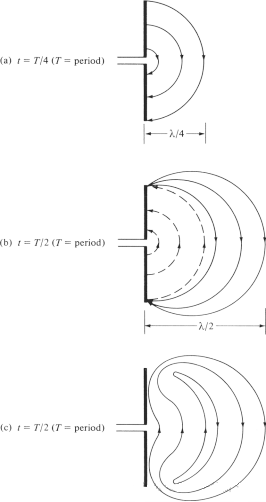
Ffigur 6
I ddysgu mwy am antenâu, ewch i:
Amser postio: 20 Mehefin 2024










